Arithmetic Progression Class 10 Ncert Solutions Pdf
Here on AglaSem Schools, you can access to NCERT Book Solutions in free pdf for Maths for Class 10 so that you can refer them as and when required. The NCERT Solutions to the questions after every unit of NCERT textbooks aimed at helping students solving difficult questions.
For a better understanding of this chapter, you should also see summary of Chapter 5 Arithmetic Progressions , Maths, Class 10.
Class 10, Maths chapter 5, Arithmetic Progressions solutions are given below in PDF format. You can view them online or download PDF file for future use.
Did you find NCERT Solutions Class 10 Maths chapter 5 Arithmetic Progressions helpful? If yes, please comment below. Also please like, and share it with your friends!
NCERT Solutions Class 10 Maths chapter 5 Arithmetic Progressions- Video
You can also watch the video solutions of NCERT Class10 Maths chapter 5 Arithmetic Progressions here.
If you liked the video, please subscribe to our YouTube channel so that you can get more such interesting and useful study resources.
Download NCERT Solutions Class 10 Maths chapter 5 Arithmetic Progressions In PDF Format
You can also download here the NCERT Solutions Class 10 Maths chapter 5 Arithmetic Progressions in PDF format.
Click Here to download NCERT Solutions for Class 10 Maths chapter 5 Arithmetic Progressions
Question & Answer
Q.1: In which of the following situations, does the list of numbers involved make an arithmetic progression, and why? (i) The taxi fare after each km when the fare is ₹ 15 for the first km and ₹ 8 for each additional km. (ii) The amount of air present in a cylinder when a vacuum pump removes \(\frac{1}{4}\) of the air remaining in the cylinder at a time. (iii) The cost of digging a well after every metre of digging, when it costs ₹ 150 for the first metre and rises by ₹ 50 for each subsequent metre. (iv) The amount of money in the account every year, when ₹ 10000 is deposited at compound interest at 8 % per annum. Ans : (i) It can be observe that Taxi fare for \( 1^{st} \) km = 15 Taxi fare for first 2 km = 15 + 8 = 23 Taxi fare for first 3 km = 23 + 8 = 31 Taxi fare for first 4 km = 31 + 8 = 39 Clearly 15, 23, 31, 39.… forms an A.P. because every term is 8 more than the preceding term (ii) Let the initial volume of air in a cylinder be V lit. In each stroke, the vacuum pump removes \(\frac{1}{4}\) of air remaining in the cylinder at a time. In other words, after every stroke ,only \(1-\frac{1}{4}=\frac{3}{4} t h\) part of air will remain. Therefore, volumes will be \(V\left(\frac{3 V}{4}\right) \cdot\left(\frac{3}{4} V\right)^{2} \cdot\left(\frac{3}{4} V\right)^{3} \dots\) Clearly, it can be observed that the adjacent terms of this series do not have the same difference between them. Therefore, this is not an A.P (iii) Cost of digging for first metre = 150 Cost of digging for first 2 metres = 150 + 50 = 200 Cost of digging for first 3 metres = 200 + 50 = 250 Cost of digging for first 4 metres = 250 + 50 = 300 Clearly, 150, 200, 250, 300 forms an A.P. because every term is 50 more than the preceding term. (iv) We know that if Rs P is deposited at r% compound interest per annum for n years, our money will be \(\mathbf{P}\left(1+\frac{r}{100}\right)^{n}\) after n years. Therefore, after every year, our money will be \(10000\left(1+\frac{8}{100}\right), 10000\left(1+\frac{8}{100}\right)^{2}, 10000\left(1+\frac{8}{100}\right)^{3}, 10000\left(1+\frac{8}{100}\right)^{4}\) Clearly, adjacent terms of this series do not have the same difference between them. Therefore, this is not an A.P.
Q.2: Write first four terms of the AP, when the first term a and the common difference d are given as follows: (i) a = 10, d = 10 (ii) a = –2, d = 0 (iii) a = 4, d = – 3 (iv) a = – 1, d = 1/2 (v) a = – 1.25, d = – 0.25 Ans : \( a=10, d=10 \) Let the series \(a_{1}, a_{2}, a_{3}, a_{4}, a_{5} \ldots \) \( \begin{array}{l}{a_{1}=a=10} \\ {a_{2}=a_{1}+d=10+10=20} \\ {a_{3}=a_{2}+d=20+10=30} \\ {a_{4}=a_{3}+d=30+10=40} \\ {a_{5}=a_{4}+d=40+10=50}\end{array} \) Therefore , the series will be 10,20,30,40,50.. First four terms of this A.P. will be 10, 20, 30, and 40. (ii) \( a=-2, d=0 \) Let the series \( a_{1,} a_{2}, a_{3}, a_{4} \dots \) \( \begin{array}{l}{a_{1}=a=-2} \\ {a_{2}=a_{1}+d=-2+0=-2} \\ {a_{3}=a_{2}+d=-2+0=-2} \\ {a_{4}=a_{3}+d=-2+0=-2}\end{array} \) Therefore the series will be \( -2,-2,-2,-2 \ldots\) First four terms of this AP. Will be \( -2,-2,-2 \text { and }-2 \) (iii) \( a=4, d=-3 \) Let the series be \( a_{1}, a_{2}, a_{3 r} a_{4} \dots \) \( \begin{array}{l}{a_{1}=a=4} \\ {a_{2}=a_{1}+d=4-3=1} \\ {a_{3}=a_{2}+d=1-3=-2} \\ {a_{4}=a_{3}+d=-2-3=-5}\end{array} \) (iv) \(a=-1, d=\frac{1}{2} \) Let the series be \( a_{1}, a_{2}, a_{3}, a_{4} \dots \) \( \begin{array}{l}{a_{1}=a=-1} \\ {a_{2}=a_{1}+d=-1+\frac{1}{2}=-\frac{1}{2}} \\ {a_{3}=a_{2}+d=-\frac{1}{2}+\frac{1}{2}=0} \\ {a_{4}=a_{3}+d=0+\frac{1}{2}=\frac{1}{2}}\end{array} \) Clearly the series will be \( -1,-\frac{1}{2}, 0, \frac{1}{2} \) Four terms of this A.P. will be \( -1,-\frac{1}{2}, 0 \text { and } \frac{1}{2} \) (v) \( a=-1.25, d=-0.25\) Let the series be \( a_{1}, a_{2}, a_{3 r} a_{4} \dots \) \( \begin{array}{l}{a_{1}=a=-1.25} \\ {a_{2}=a_{1}+d=-1.25-0.25=-1.50} \\ {a_{3}=a_{2}+d=-1.50-0.25=-1.75}\end{array} \) \(a_{4}=a_{3}+d=-1.75-0.25=-2.00 \) Clearly the series will be \( 1.25,-1.50,-1.75,-2.00 \ldots \ldots . \) First four terms of this A.P will be \( -1.25,-1.50,-1.75 \text { and }-2.00 \)
Q.3: For the following APs, write the first term and the common difference: \( \begin{array}{l}{\text { (i) } 3,1,-1,-3 \ldots} \\ {\text { (ii) }-5,-1,3,7 \ldots} \\ {\text { (iii) } 3, \frac{5}{3}, \frac{9}{3}, \frac{13}{3} \ldots} \\ {\text { (iv) } 0.6,1.7,2.8,3.9 \ldots}\end{array} \) Ans : (i) \( 3,1,-1,-3 \ldots \) Here, first term, a = 3 Common difference, d = Second term — First term = 1-3=-2 (ii) \(-5,-1,3,7 \ldots \) Here, first term, a = —5 Common difference, d = Second term — First term \( =(-1)-(-5)=-1+5=4 \) (iii) \( \frac{1}{3}, \frac{5}{3}, \frac{9}{3}, \frac{13}{3} \ldots \) Here, first term \( a=\frac{1}{3} \) Common difference, d = Second term — First term \( =\frac{5}{3}-\frac{1}{3}=\frac{4}{3} \) (iv) \( 0.6,1.7,2.8,3.9 \ldots \) Here, first term , a=0.6 Common difference, d = second term - First term \( \begin{array}{l}{=1.7-0.6} \\ {=1.1}\end{array} \)
Q.4: Which of the following are APs? If they form an AP, find the common difference d and write three more terms. (i) \( 2,4,8,16, \dots \) (ii) \( 2, \frac{5}{2}, 3, \frac{7}{2}, \ldots \) (iii) \( -1.2,-3.2,-5.2,-7.2, \dots \) (iv) \(-10,-6,-2,2, \dots \) (v) \( 3,3+\sqrt{2}, 3+2 \sqrt{2}, 3+3 \sqrt{2}, \ldots \) (vi) \( 0.2,0.22,0.222,0.2222 \) (vii) \( 0,-4,-8,-12, \dots \) (viii) \( -\frac{1}{2},-\frac{1}{2},-\frac{1}{2},-\frac{1}{2}, \ldots \) (ix) \( 1,3,9,27, \dots \) (x) \( a, 2 a, 3 a, 4 a, \dots \) (xi) \( a, a^{2}, a^{3}, a^{4}, \dots \) (xii) \( \sqrt{2}, \sqrt{8}, \sqrt{18}, \sqrt{32}, \dots \) (xiii) \(\sqrt{3}, \sqrt{6}, \sqrt{9}, \sqrt{12}, \dots \) (xiv) \( \mathrm{1}^{2}, 3^{2}, 5^{2}, 7^{2}, \ldots \) (xv) \(1^{2}, 5^{2}, 7^{2}, 73, \dots \) Q.5: Fill in the blanks in the following table, given that a is the first term, d the common difference and an the nth term of the AP 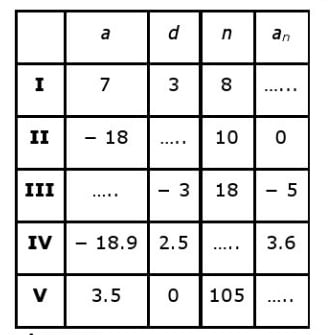
Ans : (I) \( a=7, d=3, n=8, a_{n}=? \) We know that , For an A.P \( a_{n}=a+(n-1) d \) \( \begin{array}{l}{=7+(8-1) 3} \\ {=7+(7) 3} \\ {=7+21=28}\end{array}\) Hence \( a_{n}=28 \) (II) Given that \( a=-18, n=10, a_{n}=0, d=? \) We know that \( a=-18, n=10, a_{n}=0, d=? \) We know that \( \begin{array}{l}{a_{n}=a+(n-1) d} \\ {0=-18+(10-1) d} \\ {18=9 d} \\ {d=\frac{18}{9}=2}\end{array} \) Hence common difference , d=2 (III) Given that \( d=-3, n=18, a_{n}=-5 \) We know that \( \begin{array}{l}{a_{n}=a+(n-1) d} \\ {-5=a+(18-1)(-3)} \\ {-5=a+(17)(-3)} \\ {-5=a-51} \\ {a=51-5=46}\end{array} \) Hence a=46 (IV) \( a=-18.9, d=2.5, a_{n}=3.6, n=? \) We know that \( \begin{array}{l}{a_{n}=a+(n-1) d} \\ {3.6=-18.9+(n-1) 2.5} \\ {3.6+18.9=(n-1) 2.5} \\ {22.5=(n-1) 2.5} \\ {(n-1)=\frac{22.5}{2.5}} \\ {n-1=9} \\ {n=10}\end{array} \) Hence, n=10 (V) \( a=3.5, d=0, n=105, a_{n}=? \) We know that \( \begin{array}{l}{a_{n}=a+(n-1) d} \\ {a_{n}=3.5+(105-1) 0} \\ {a_{n}=3.5+104 \times 0} \\ {a_{n}=3.5} \\ {\text { Hence, } a_{n}=3.5}\end{array} \)
NCERT / CBSE Book for Class 10 Maths
You can download the NCERT Book for Class 10 Maths in PDF format for free. Otherwise you can also buy it easily online.
- Click here for NCERT Book for Class 10 Maths
- Click here to buy NCERT Book for Class 10 Maths
All NCERT Solutions Class 10
- NCERT Solutions for Class 10 English
- NCERT Solutions for Class 10 Hindi
- NCERT Solutions for Class 10 Maths
- NCERT Solutions for Class 10 Science
- NCERT Solutions for Class 10 Social Science
- NCERT Solutions for Class 10 Sanskrit
All NCERT Solutions
You can also check out NCERT Solutions of other classes here. Click on the class number below to go to relevant NCERT Solutions of Class 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12.
| Class 1 | Class 2 | Class 3 |
| Class 4 | Class 5 | Class 6 |
| Class 7 | Class 8 | Class 9 |
| Class 10 | Class 11 | Class 12 |
Download the NCERT Solutions app for quick access to NCERT Solutions Class 10 Maths Chapter 5 Arithmetic Progressions. It will help you stay updated with relevant study material to help you top your class!
Arithmetic Progression Class 10 Ncert Solutions Pdf
Source: https://schools.aglasem.com/ncert-solutions-class-10-maths-chapter-5/